Overview
The overarching goal of our research is to understand how quantum physics can be exploited to develop new technologies that are otherwise impossible. Over the past few decades, it was discovered that quantum physics has the potential to revolutionize information security and sensor technology, in addition to enabling quantum computers, devices capable of solving a number of outstanding problems in physics, chemistry, and biomedicine that are intractable with even the most powerful supercomputers. These findings have spurred enormous efforts around the world to bring these quantum information technologies to fruition.

Our research is focused on bridging the gap between abstract theory and experimental reality. Most of the basic principles underlying quantum information technologies are well understood at this point, and the central challenge now is to determine how real physical systems can be identified and developed to realize these technologies in the laboratory despite their imperfections. Our research group uses a combination of analytical and numerical methods to understand and tackle a range of problems in quantum information science. While our work is purely theoretical, we often provide support to experimental groups around the world. Areas of primary focus include the development of control techniques for quantum processors based on semiconductors, low-temperature superconducting electronic circuits, or atomic systems; the development of microscopic models of how quantum systems interact with their environment that can be used to learn how to either suppress such interactions or exploit them for technological applications; the design of protocols that leverage quantum mechanics to achieve secure, long-distance communication and computation using photonic qubits; the development of circuit-based and pulse-based quantum algorithms for simulating many-body quantum systems and chemical systems, for solving classical optimization problems, and for other applications; and the study of quantum many-body dynamics, entanglement generation, and non-equilibrium phases of matter.

Quantum computing
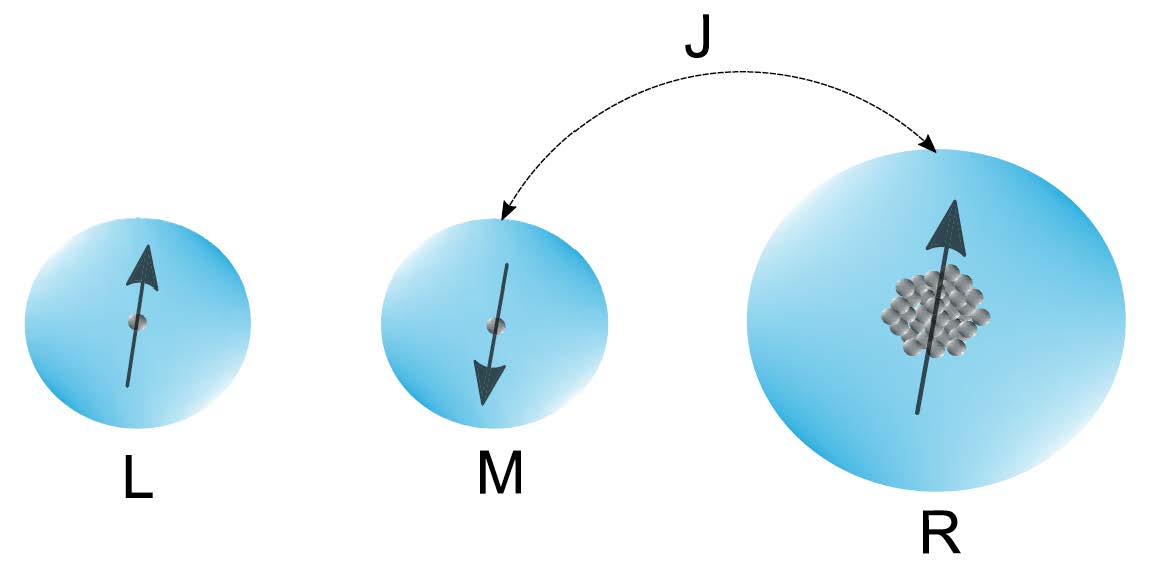Quantum mechanics offers the potential to revolutionize the way in which information is stored, transferred, and processed. The two main challenges are decoherence (the loss of information due to unwanted interactions between a quantum system and its environment) and scalability (can a large number of microscopic quantum systems be connected together and controlled with the requisite precision?). Much of our work is devoted to solving both of these problems for a number of different physical systems that are currently at the forefront of quantum information science research. Leading platforms include semiconductor spin qubits, qubits based on superconducting circuits, qubits based on trapped neutral atoms or ions, and photonic qubits. Our group studies decoherence, scalability, and other important issues that relate to the hardware of quantum computing. Our group also works on measurement-based quantum computing, which is a popular approach in photonic systems. In this approach, highly entangled multi-photon resource states are generated upfront, and quantum computations are carried out by performing measurements on the photons. Here, the main challenges are to efficiently produce the requisite resource states while mitigating photon loss and other errors.

Quantum control
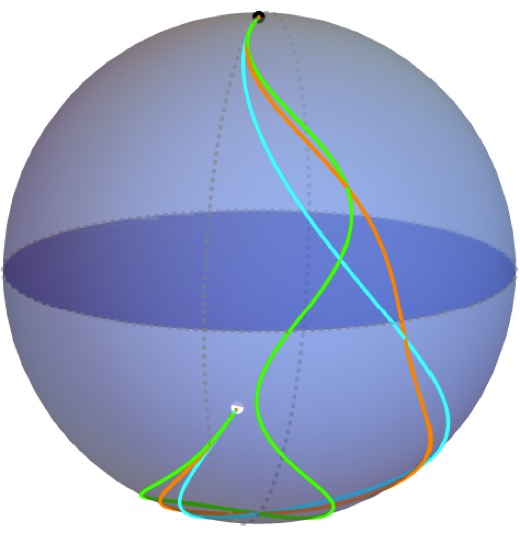Harnessing the power of quantum mechanics and integrating it into new technologies is a long-standing goal in the fields of quantum information and nanoscience. The main obstacle to realizing such quantum technologies is decoherence. In addition to making advancements in the design and fabrication of nanoscale systems, overcoming this problem requires the development of control protocols capable of maintaining or manipulating the quantum information stored in these systems while simultaneously mitigating the deleterious effects of the environment. This task is made challenging by the fact that developing such control protocols requires one to solve the time-dependent Schrodinger equation, which is generally intractable analytically---only a handful of exact solutions have been found since the birth of quantum mechanics almost one hundred years ago. To overcome this problem, we developed a way to construct an infinite number of solutions using a reverse-engineering technique. In addition, we developed a new mathematical framework that allows one to visualize in a simple geometrical way the entire solution space of control protocols that suppress adverse environmental effects. We are using this method to design robust quantum logic gates in a variety of qubit platforms. We have further extended our analytical control techniques to address another type of control problem known as leakage, which can become significant when multiple quantum systems are coupled together.

Quantum algorithms and simulation
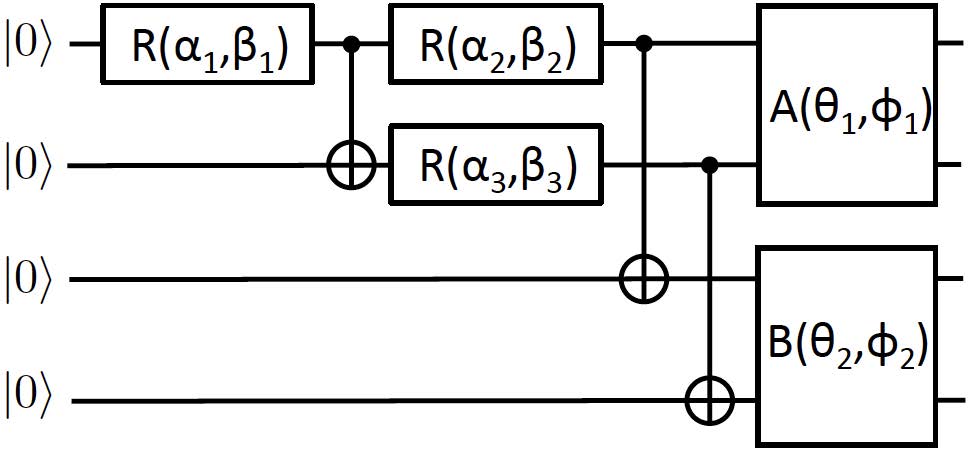While the simulation of quantum systems on today's classical computers has been tremendously successful, large, strongly correlated quantum systems remain far beyond the reach of the world's best supercomputers. This is due to the inability of classical machines to store or manipulate exponentially large quantum states. The concept of digital quantum simulation proposes to circumvent this problem by replacing the classical computer with a programmable quantum processor built from qubits. Quantum simulation is believed to be one of the most near-term applications of quantum information science in that a modest-sized quantum processor containing as few as 50-100 qubits may be sufficient to simulate systems that are classically intractable. Realizing this potential requires simultaneous advancements in qubit hardware and in simulation algorithms. Our research focuses on developing new, efficient algorithms for quantum simulation that reduce the number of qubits and the number of logic gates needed to extract the desired information from the system being simulated such as energy eigenvalues and eigenstates. We also work closely with experimental groups to determine the control schemes and device architectures that are optimal for achieving efficient, accurate simulations. In addition to simulation, we also develop quantum algorithms for other applications such as classical optimization problems.

Quantum communication and networks
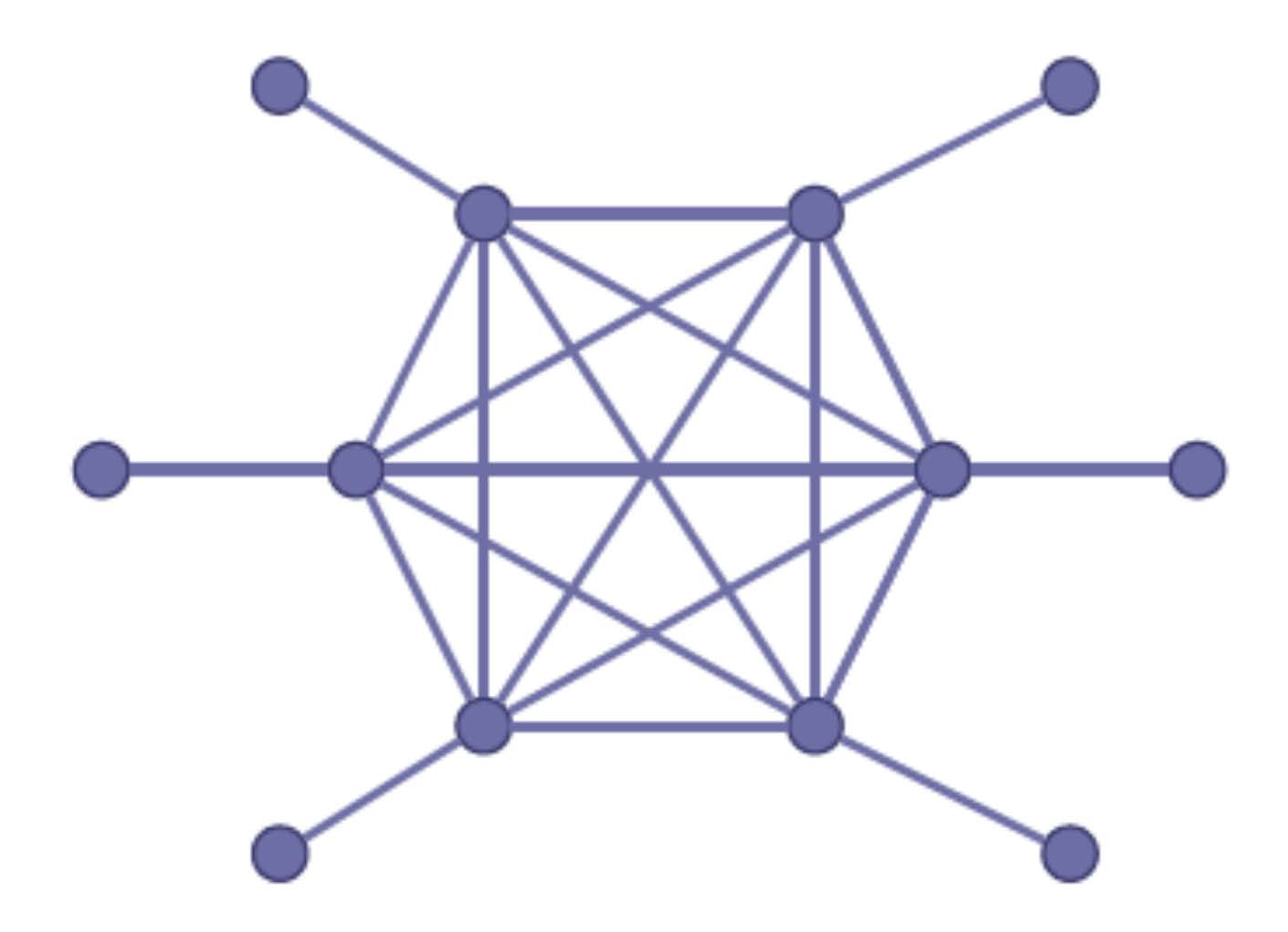Future powerful quantum computers will be capable of running algorithms that can be used to crack the RSA encryption system---the predominant scheme used to protect sensitive data and internet transactions across the world. Although quantum mechanics can be used to compromise information security in this way, it also offers a way to defend against such attacks. The quantum no-cloning theorem, which forbids the copying of unknown quantum states, implies that it is possible to transmit information in a way that makes it impossible to intercept transmissions without being detected. This idea has lead to the notion of quantum communication, which aims to develop communication networks that are immune to hacking, even by large-scale quantum computers. While the no-cloning theorem is the basic principle that makes quantum communication possible, it also poses a challenge. Transmitting information over long distances generally requires that the information be copied and re-amplified at multiple points (repeaters) along the information path due to the lossiness of optical fibers. However, the no-cloning theorem prevents a direct implementation of this idea in the case of quantum information. Quantum entanglement can be used to get around this problem. We are developing schemes to produce complex, entangled states of light for long-distance quantum communication networks. This effort is based on our recent theoretical finding that the complex states needed for distributing information securely across networks can be produced using only a few quantum emitters. We are working with our experimental collaborators to construct and test photonic circuit devices capable of implementing this idea.

Quantum many-body dynamics
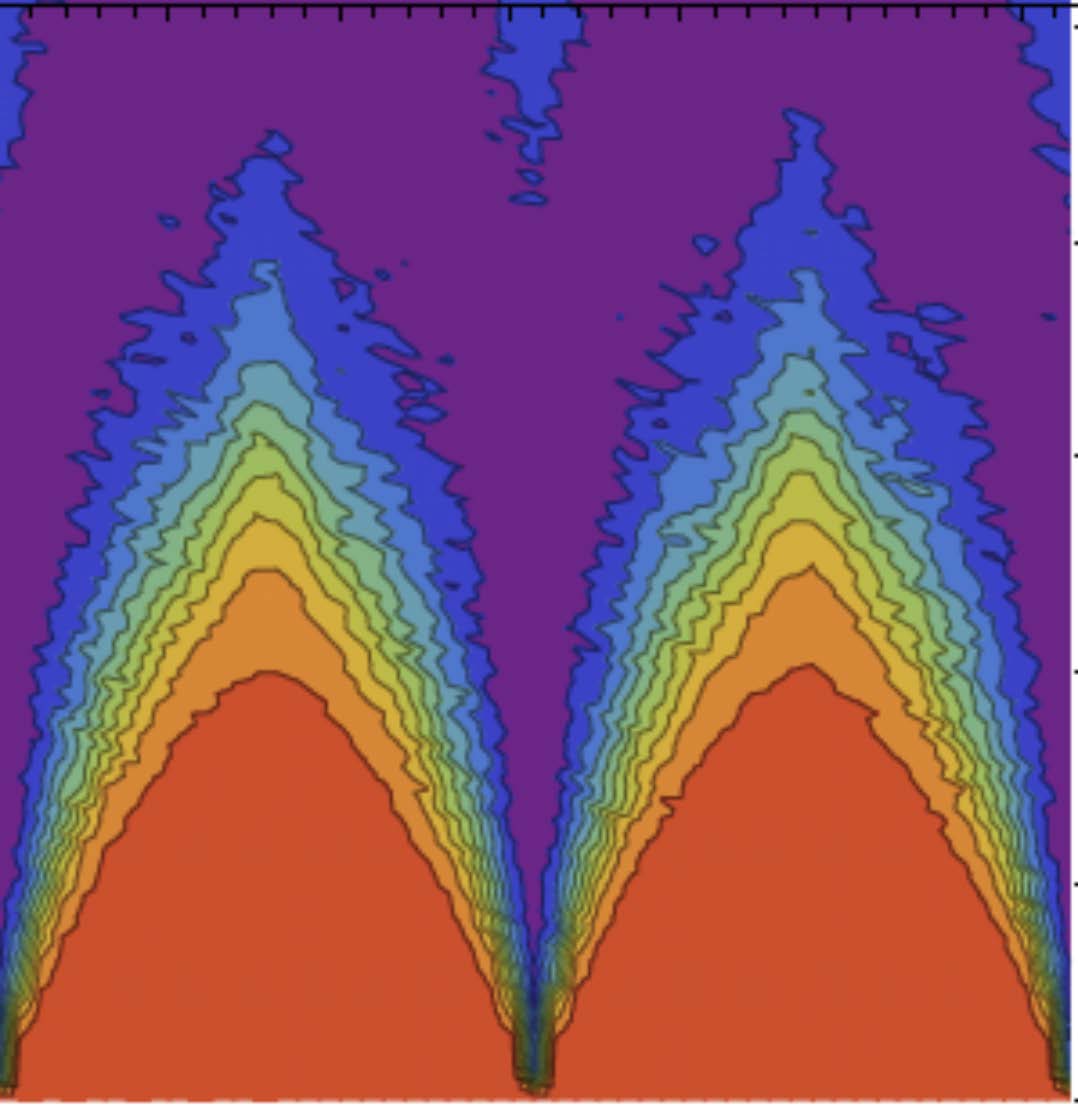Most interacting quantum many-body systems will act like their own thermal baths in the sense that any subsystem will approach thermal equilibrium on long timescales, erasing any memory of the initial state. However, in recent years a number of interacting systems have been shown to violate this expectation, even in the presence external driving, which one would naively expect to cause heating and eventually the formation of a thermal state. Some of the phases which exhibit this type of behavior are known as many-body localization and time crystals. We are interested in better understanding when such phases arise and how they can be used to enhance the coherence times of qubits. We primarily investigate interacting spin models to answer these questions, and we collaborate closely with experimental groups working on spin systems to realize these phases in the laboratory. We have shown that signatures of many-body localization are evident in systems containing as few as four spins, and that these signatures can be detected using existing experimental techniques. We have also shown that applying periodic driving to such a system can create a discrete time crystal phase in which the spins periodically return to their initial state despite the presence of spin-spin coupling, control errors, and local disorder. We are working to exploit this behavior to extend the coherence times of spin systems for the purpose of quantum information processing.