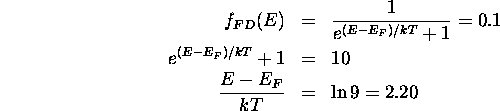
Physics 3304 Assignment 10 solutions

Grading: The problems that will be graded in detail for this assignment are Ch. 11, problems 18 and 25 (each worth 5 points total). You will receive 1 point for each of the other problems if you have made a reasonable attempt at a solution. (Total points for this assignment=17)

Ch. 11, Problem 15

a)

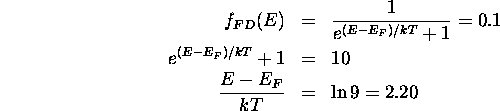
At room temperature (300 K), 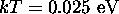, so

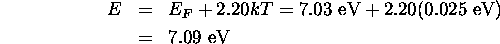
b) 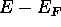is 2.20 times kT.

Ch. 11, Problem 16

The electron has a kinetic energy equal to the Fermi energy for copper (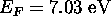). Since the kinetic energy is much less than the rest energy of the electron, it is valid to use the non-relativistic relation between kinetic energy and momentum:

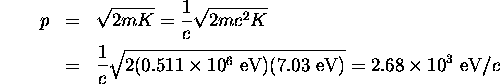
The de Broglie wavelength is given by:

This is comparable to the atomic spacing of copper (0.256 nm).

Ch. 11, Problem 17

This problem should have read "what is the number of conduction electrons per unit volume in sodium with energies between 0.10 eV and 0.11 eV above the Fermi energy". Equation 10.36 of Chapter 10 gives us the number of electrons with energy between E and E+dE (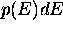). Dividing this expression by the volume of the system, V, gives us the desired expression:

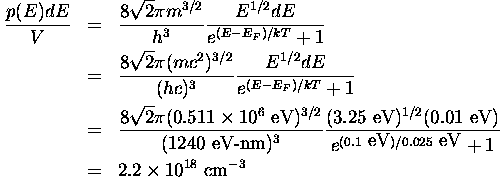
Ch. 11, Problem 18

The Fermi energy is given by:

The density of free electrons is:

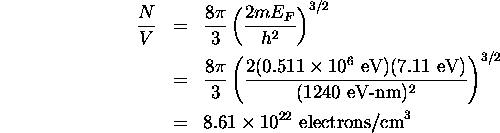
The number density of magnesium atoms is given by:

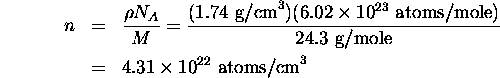
So the number of free electrons per atom is:

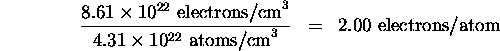
Ch. 11, Problem 19

The temperature dependence of the Fermi energy can be expressed as:

This is much higher than the melting temperature of gold (7076 K), so for most practical purposes we can assume that the Fermi energy is constant when doing calculations.

Ch. 11, Problem 20

Since zinc has two conduction electrons per atom, the conduction electron density is twice the atomic density:

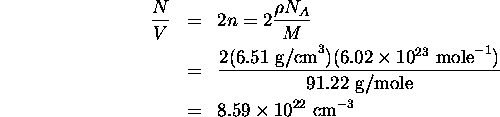
So the Fermi energy is:

Ch. 11, Problem 22

The Wiedemann-Franz law gives a relation between the thermal and electrical conductivity of a metal:

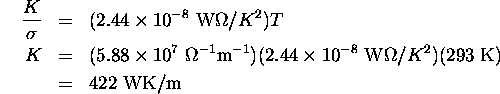
Ch. 11, Problem 24

a) The number of electrons excited across the gap is given by the total energy of the photon divided by the gap energy:

b) The statistical fluctuations in N are given by:

and the fractional variation in N is:

c) The energy is proportional to the number of detected electrons, so

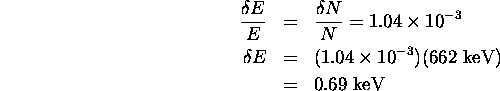
Ch. 11, Problem 25

a) For a state at the top of the valence band, 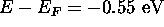so

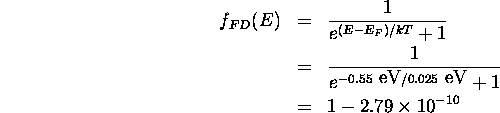
b) For a state at the bottom of the conduction band, 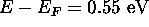so

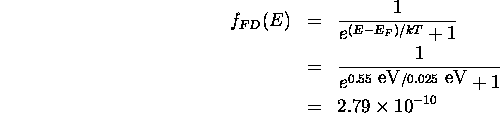
c) At 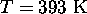, 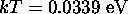and

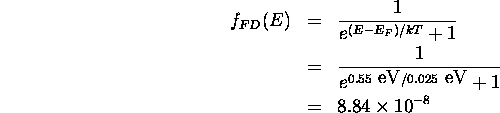
so the probabilities are 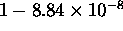and 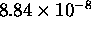.