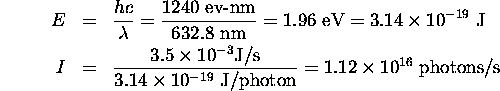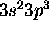
Physics 3304 Assignment 8 solutions
Grading: The problems that will be graded in detail for this assignment are Ch. 8, problems 3 and 12 (each worth 5 points total). You will receive 1 point for each of the other problems if you have made a reasonable attempt at a solution. (Total points for this assignment=18)
Ch. 8, Problem 2
a) [Ne]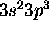
b) [Ar]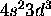
c) [Kr]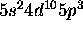
d) [Xe] 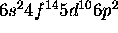
Ch. 8, Problem 3
For sodium the ionization energy is 5.14 eV and the outermost
electron is in an n=3 state. To estimate the effective
nuclear charge we can picture this as a single-electron atom with central
charge  . Then we have:
. Then we have:
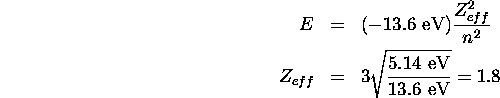
For potassium the ionization energy is 4.34 eV and the electron is in an n=4 state.

In the Bohr model the orbit of the outermost electron is completely outside
the inner electrons, so we would expect the inner electrons (Z-1 of them)
to provide complete screening, which means 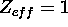 .
.
Ch. 8, Problem 4
Applying Equation 6.42 to an atom with Z-1 nuclear charge, we obtain
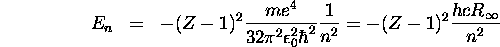
using Equation 6.40 for 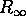 . The frequency of the emitted radiation
is
. The frequency of the emitted radiation
is
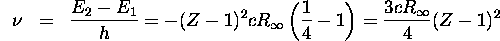
Ch. 8, Problem 5
Solving Equation 8.1 with 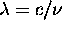 gives:
gives:
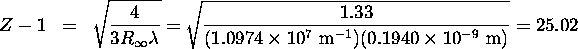
Thus Z=26 and the element is iron.
Ch. 8, Problem 10
Cr: [Ar]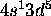
There is nothing that prevents all 6 electrons from having 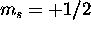 , and
thus
, and
thus 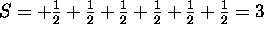 . The Pauli principle forces the five 3d electrons to have
different
. The Pauli principle forces the five 3d electrons to have
different 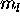 values, which are +2,+1,0,-1,-2; the 4s electron has
values, which are +2,+1,0,-1,-2; the 4s electron has
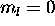 only. The total L is therefore L=+2+1+0-1-2+0=0. The ground
state therefore has L=0 and S=3.
only. The total L is therefore L=+2+1+0-1-2+0=0. The ground
state therefore has L=0 and S=3.
Ch. 8, Problem 11
a) Ce: [Xe]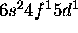
The 6s subshell is full. The 4f and 5d electron can each have
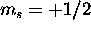 for a total S of 1. The Pauli principle does not
prevent the
for a total S of 1. The Pauli principle does not
prevent the 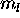 values of these two electrons from having their maximum
possible values of +3 (for 4f) and +2 (for 5d). Thus L=2+3=5. The
ground state is thus L=5,S=1.
values of these two electrons from having their maximum
possible values of +3 (for 4f) and +2 (for 5d). Thus L=2+3=5. The
ground state is thus L=5,S=1.
b) Gd: [Xe]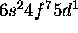
The 6s subshell is full. To maximize S, we give all seven 4f electrons
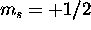 (which is possible, because the 4f shell has a capacity of 14)
and we also give
(which is possible, because the 4f shell has a capacity of 14)
and we also give 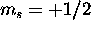 to the 5d electron. Thus S=8(1/2)=4. The
Pauli principle requires that all seven of the 4f electrons have
different
to the 5d electron. Thus S=8(1/2)=4. The
Pauli principle requires that all seven of the 4f electrons have
different 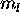 values, which are
values, which are 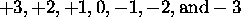 for a total
of 0. The only contribution to L comes from the 5d electron,
which contributes
for a total
of 0. The only contribution to L comes from the 5d electron,
which contributes 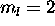 . The ground state is therefore L=2,S=4.
. The ground state is therefore L=2,S=4.
c) Pt: [Xe]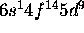
The 4f subshell is full. The spin of the nine 5d electrons is maximized
by giving five of them 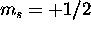 and the remaining four
and the remaining four 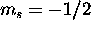 . The
6s electron also contibutes
. The
6s electron also contibutes 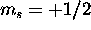 , for a total of S=1. The 6s
electron doesn't contibute to L, and the five 5d electrons with
, for a total of S=1. The 6s
electron doesn't contibute to L, and the five 5d electrons with 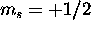 have
have 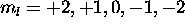 and give no net contribution to L. We therefore
maximize the contribution to L of the remaining four 5d electrons by
assigning them
and give no net contribution to L. We therefore
maximize the contribution to L of the remaining four 5d electrons by
assigning them 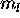 of +2,+1,0,-2 for a net total of L=2. The ground
state is thus L=2,S=1.
of +2,+1,0,-2 for a net total of L=2. The ground
state is thus L=2,S=1.
Ch. 8, Problem 12
a) F: [He]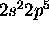
The 2s subshell is full. For the five 2p electrons, the total spin
is maximized by having three with 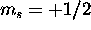 and the remaining two with
and the remaining two with
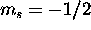 which gives
which gives 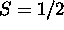 . The Pauli principle requires that the
three
. The Pauli principle requires that the
three 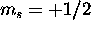 electrons have
electrons have 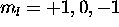 for a total of zero. The
two
for a total of zero. The
two 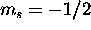 electrons maximize L if assigned
electrons maximize L if assigned 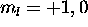 . Thus
. Thus
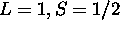 for the ground state.
for the ground state.
b) Mg: [Ne]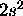
The 2s subshell is full so L=0,S=0 for the ground state.
c) Ti: [Ar]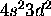
The 4s subshell is full. Maximizing S for the 3d electrons gives
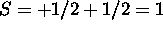 . The 3d electrons must have different
. The 3d electrons must have different 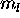 , and so
L is maximized with
, and so
L is maximized with 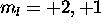 . Thus L=3,S=1 for the ground state.
. Thus L=3,S=1 for the ground state.
d) Fe: [Ar]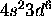
The 4s subshell is full. Maximizing S for the 3d electrons gives
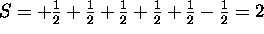 . The five electrons with
. The five electrons with 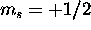 are assigned
are assigned 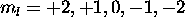 , and
the electron with
, and
the electron with 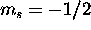 has
has 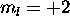 . Thus L=2,S=2 for the ground
state.
. Thus L=2,S=2 for the ground
state.
Ch. 8, Problem 13
Each electron has 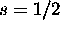 , so the total possible S is 0 or 1. The two
d electrons, each with l=2, can couple to give L=0,1,2,3,4.
, so the total possible S is 0 or 1. The two
d electrons, each with l=2, can couple to give L=0,1,2,3,4.
Ch. 8, Problem 19
a) For a 2p electron n=2,l=1; thus 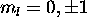 and
and 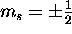 .
So the six possible sets of quantum numbers are:
.
So the six possible sets of quantum numbers are:
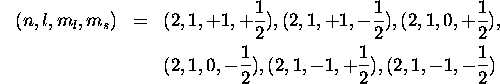
b) Since there are 6 possible sets for each electron, the total number
of possibilities for 2 electrons is 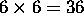 .
.
c) The Pauli principle prevents the two sets from being identical. There will be 6 combinations in which the sets are identical, which must be eliminated, leaving 30 allowed combinations.
d) Since the n values are different, the Pauli principle does not restrict the number of possible cominations, so there will be 36 possible sets.
Ch. 8, Problem 22
a) For 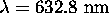 ,
,