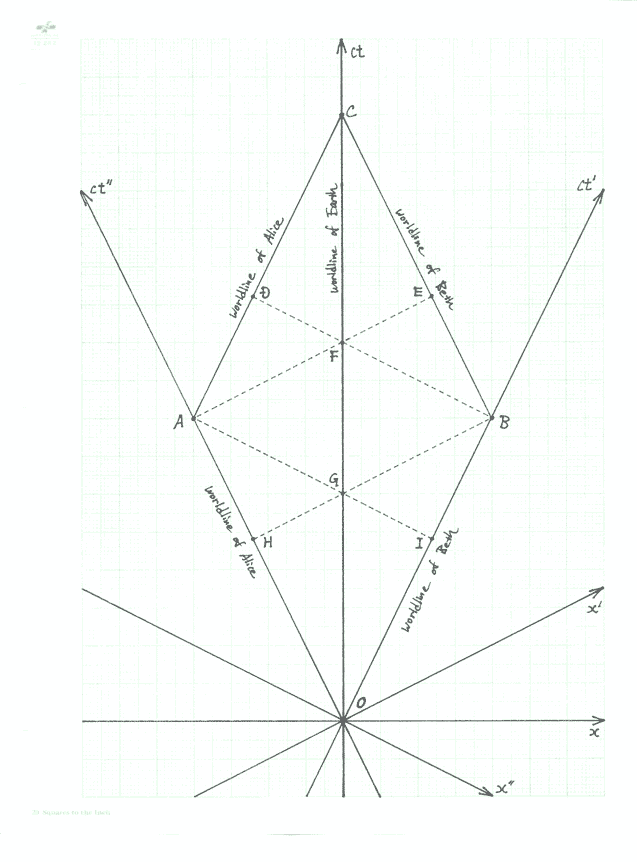
Twin Paradox

Recall the "twin paradox" that we discussed in section 15 of the lecture notes: Alice and Beth are twins. Beth travels to a far away star in a high-speed spaceship while Alice remains at home on Earth. Due to time dilation, Alice observes time to be flowing slower on Beth's spacethip than on the Earth, while Beth observes time to be flowing slower on the Earth than on her spaceship. This seems to indicate that at both sisters must find the other to be the younger of the two when Beth returns to the Earth; a clear contradiction.

The resolution to the problem lay in the fact that Beth has to turn around somewhere to come back to the Earth, and thereby jump from one inertial frame to another, while Alice stays with the Earth frame of reference throughout. This breaks the symmetry between the two sisters: from Beth's point of view, time on Earth seems to suddenly ``jump forward'' when she turns around, and as a result Beth will be younger than Alice at the conclusion of the trip.

But what if Alice and Beth were treated completely symmetrically? Consider both Alice and Beth put on high-speed spaceships and sent in opposite directions at the same speed. After traveling the same distance, both sisters turn around and head back toward the Earth at the same speed, arriving home at the same time. The worldlines of Alice and Beth are shown on the spacetime diagram. They both leave the Earth at O, with Alice heading toward the left and Beth heading toward the right. Alice turns around and heads back toward the Earth at A, while Beth turns around and heads back toward the Earth at B. They both return to the Earth at C.

During the trip, Alice observes time to be flowing slower in Beth's spaceship than in her own, while Beth observes the exact opposite. Does this mean that both sisters must find the other to be the younger of the two at the end of their trip at C? Would there not be a contradiction this time since there is nothing to break the symmetry?

Answer the following questions:

1. Which spacetime point along Beth's worldline is simultaneous with A in the frame that Alice was in before she turned around?
2. Which spacetime point along Beth's worldline is simultaneous with A in the frame that Alice was in after she turned around?
3. Which sister will be older at the conclusion of the trip at C? Explain, referring to the spacetime diagram.