13. Lorentz Contraction

Next, let's think about the measurement of length.

First, ponder for a moment what we mean by "length". We mean the distance between both ends of an object "at the same time", don't we?

Say, we wanted to measure the length of a moving train. We wouldn't measure the position of the front end of the train at one time, and the position of the back end of the train at another time, and then take the difference, would we? The train would have moved in between the two times and what we get would not be what we think of as its length.

But we have been discussing that the concept of simultaneity depends on the observer!

Consider the spacetime diagram below. The observer riding the train would record the position of the front end of the train and the position of the back end of the train "at the same time" in the train frame and obtain the length of the train, L', by taking the difference. But the observer on the ground would record the position of the front end of the train and the position of the back end of the train "at the same time" in the ground frame and obtain what he thinks is the length of the train, L, which is clearly shorter than L' !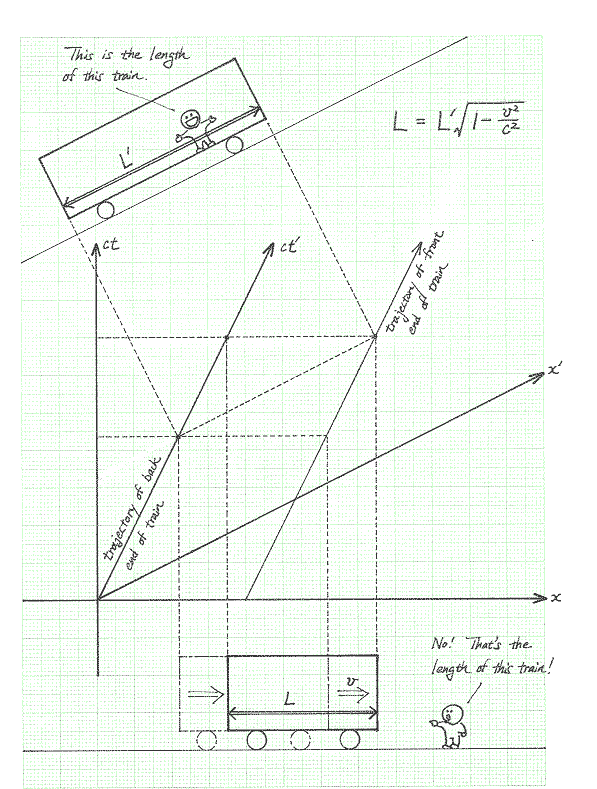

Spacetime Diagram explanation of Lorentz Contraction

Since what we think of as the natural length of an object is its length at rest, we can conclude that moving objects look shorter than their natural lengths at rest. This is called Lorentz contraction. Using the Lorentz transformation formula, we can find that the ratio of contraction is given by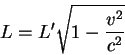

where L' is the natural length of the object at rest and L is its observed length when it is moving at speed v. (The ' on L' is to show that it is the length observed in the moving frame in which the object is at rest.)

Back to Table of Contents

Previous  Next