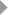
Twin Paradox - Solution

1. I.
2. E.
3. Alice and Beth will be of the same age at C.
   As Alice travels from O to A on the outbound portion of her trip, she observes the time in Beth's spaceship to pass from O to I, which is shorter than the time from O to A in Alice's frame. During the inbound portion of her trip from A to C, Alice observes the time in Beth's spaceship to pass from E to C, which is again shorter than the time from A to C in Alice's frame. However, when Alice turns around at A to switch inertial frames, the point along Beth's worldline which is simultaneous with A jumps forward from I to E, which cancels out the time dilation effect.
   Similarly, as Beth travels from O to B on the outbound portion of her trip, she observes the time in Alice's spaceship to pass from O to H, which is shorter than the time from O to B in Beth's frame. During the inbound portion of her trip from B to C, Beth observes the time in Alice's spaceship to pass from D to C, which is again shorter than the time from B to C in Beth's frame. However, when Beth turns around at B to switch inertial frames, the point along Alice's worldline which is simultaneous with B jumps forward from H to D, which cancels out the time dilation effect.
   Both Alice and Beth observe the time in the other spaceship to be flowing slower in the outbound and inbound parts of their trips, but because of the "jump forward" effect when they turn around, they will be of the same age when they meet at C.