Voronoi Diagrams
This page serves as a location where the information pertaining to the shapes of single bubbles in the group are stored.
This page serves as a location where the information pertaining to the shapes of single bubbles in the group are stored.
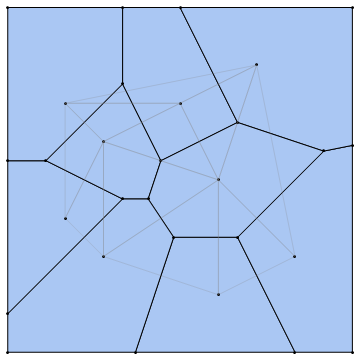
To build a Voronoi Diagram, given a series of "sites" (meaning coordinates)
on a two dimensional plane, first find the Delaunay Triangulation of the points in question. This can
be done easily in Wolfram Mathematica. See the Computing Voronoi Diagrams
for more information. After the Delaunay Triangulation of the sites have been found, put lines perpendicular bisecting the
ones made in the Delaunay Triangulation and extend them. Terminate them at intersections, should they have any.
This is graphically represented at the right.
Notice that not all of the lines created in the Delaunay Triangulation intersect with the line that
it corresponds to in the Voronoi Diagram. Although this is true, each line in the Delaunay Triangulation
corresponds to a line in the Voronoi Diagram. Although this array of cells does not in general follow
the Young-Laplace Equation nor Plateau's Laws, they have created what
vaguely looks like a foam. In each of these cells there are, of course, an infinite number of points. Each of
those points in a cell is closer to the site contained within that cell than it is to any other site, while the
cell borders are guaranteed to be equidistant from the two sites used to define it.
In order to give the Voronoi Diagrams parameters that allow them to better simulate bubbles, the points can be given weight. There are several kinds of weighting for Voronoi Diagrams, but the one that will be focused on is multiplicative weighting. This weight is akin to the pressure inside of a bubble, and the differences in weight between points are akin to the pressure gradient between bubbles. That being said, giving weight to points on the diagram causes the bisection lines to deform into circular arcs, much like bubbles do.
Voronoi Diagrams are used in the simulation of two dimensional dry foams and are a powerful tool in understanding the mechanics behind those foams. In simulations discussed by Hutzler and Weaire1, a 'base-structure' should be given as well as the boundary conditions that are applied to all of the cells. These boundary then should be able to modify the cells and allow them to equilibriate to a foam structure that satisfies them. The boundary conditions in question, of course, are the Young-Laplace Equation for a thin film and Plateau's Laws. The text discusses simulations that allow the bubbles to relax towards the boundary conditions that are applied. This is because these conditions come from local energy minimization. Once these conditions are satisfied, the model is considered to be an accurate depiction of a dry foam.
As of version 10, Wolfram Mathematica is able to generate Voronoi Diagrams using the
VoronoiMesh function. Earlier versions of Mathematica require the use of the
ComputationalGeometry package, for which the function is titled VoronoiDiagram.
Follows is some example code and to generate a random Voronoi
Diagram of 25 sites within a square ranging from (0, 0) to (10, 10).
sites = RandomReal[{0, 10}, {20, 2}]
Show[VoronoiMesh[sites], Graphics[Point[sites]]]
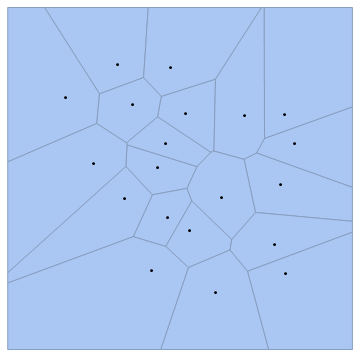
The image to the right is an example output generated by the above code. Note that this code will not work in versions
of Mathematica older than version 10. Also note that
this is only an example output. Since the points are pseudo-randomly generated each Voronoi Diagram
will be different, although will still hold 25 sites and will be bounded by the same 10 by 10 box.
To generate the associated Delaunay Triangulation, simply use the DelaunayMesh function using
the array of sites as input. For more information on these functions, see the Wolfram Mathematica
documentation on them.
1Stefan Hutzler and Denis Weaire, The Physics of Foams, (Oxford University Press, New York, 1999).